
(The reason I say the second issue is "sort of" a physical issue is that the mathematical reason given above actually eliminates this problem: To be rigorous you should always specify first a Hilbert space and then a Hamiltonian, and you will never run into ambiguities like whether the spectrum is discrete or continuous.
Hilbert space unbounded states free#
the free particle Hamiltonian $H=\frac^n$ and discrete for the torus). Physical reason (sort of): What looks like the same Hamiltonian, e.g. Without knowing a Hilbert space, it doesn't even make sense to speak of an operator on it. Let H be a separable Hilbert space and D a dense domain in H, equipped with a locally convex topology, finer than the norm topology. Mathematical reason: The Hamiltonian is an operator on a Hilbert space to begin with. This textbook provides an introduction to representations of general -algebras by unbounded operators on Hilbert space, a topic that naturally arises in quantum mechanics but has so. Colloquially speaking, the nucleon has 'leaked' or 'dripped' out of the nucleus, hence giving rise to the term 'drip line'. Basic spectral theory for unbounded operators 70 4.6. Criterion for self-adjointness and for essential self-adjointness 68 4.5. The graph, closed and closable operators 60 4.3.
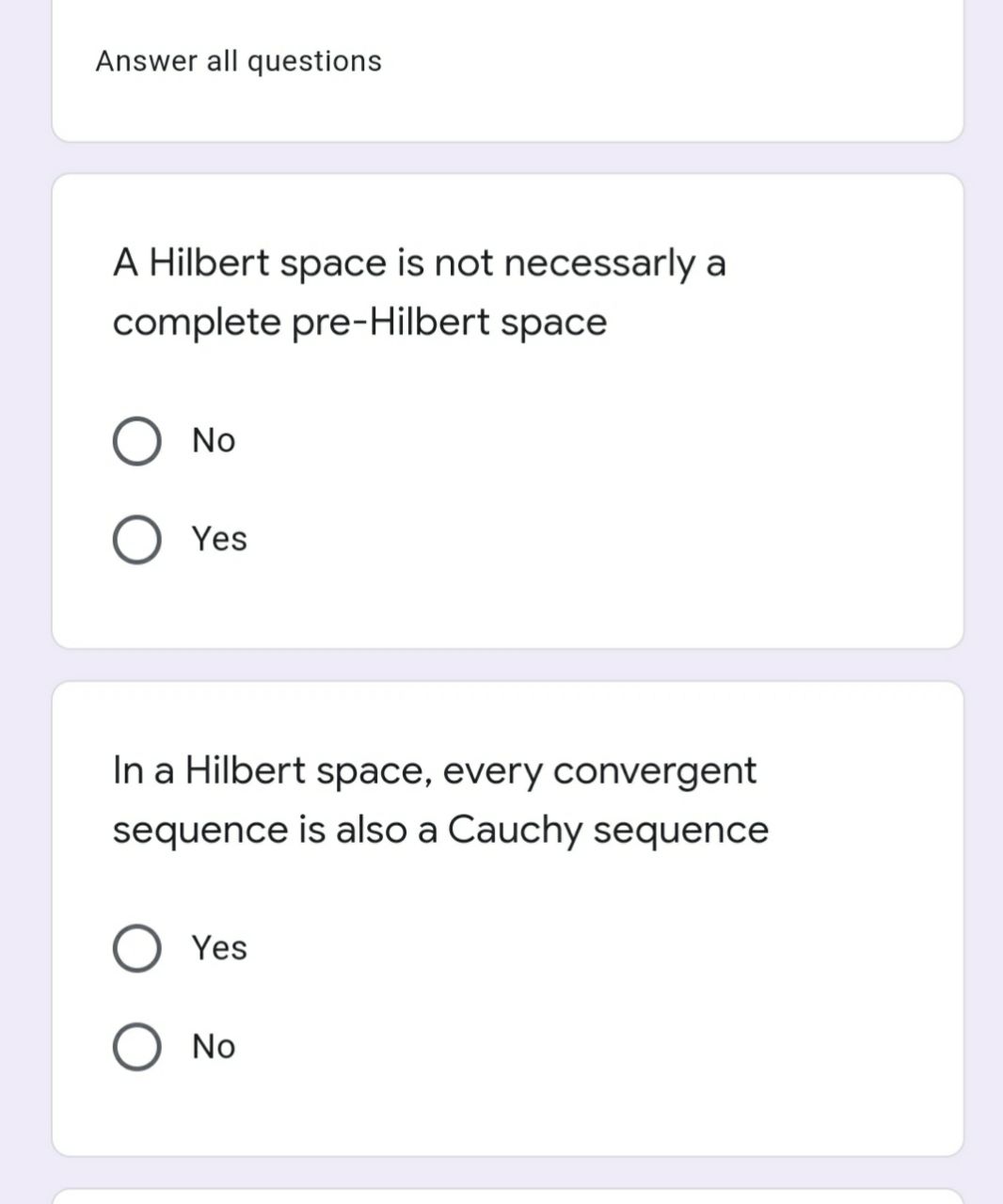
There is a mathematical reason and a (sort of) physical reason: Unbounded operators on a Hilbert space 57 4.1.


 0 kommentar(er)
0 kommentar(er)
